Lightbot is a game that allows children to learn the basics of coding.

Programming is one of the most important skills of the 21st century because it allows performing certain tasks in less time, as the computer is in charge of carrying them out using the instructions that have been programmed. This is why it is important that people who do not know how to code begin to learn practically.

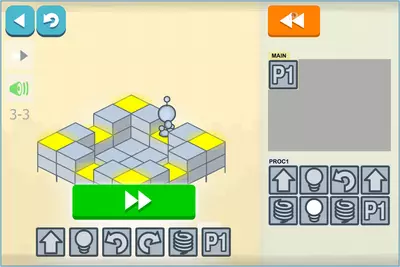
Lightbot offers a friendly environment where anyone with no previous programming knowledge can make contact and learn the basics of coding.

When we access the game, we must choose a level to start. The most logical thing is to start at the first level and move on to the next level when we finish all the stages. In level 1, basic programming concepts are taught; in level 2, we learn what a procedure or function is; in level 3, we learn the concept of a loop. The concepts learned in these levels will be applicable in real programming languages, as it will be easy to translate what we have learned into a specific programming language.

The game's objective is simple: we must give orders to a robot to move across the screen and light all the blue boxes. With this simple purpose, we will see how programming can be used to send commands and control the robot.
For example, in the beginning, we will be able to send up to 12 commands to the robot, so the robot can perform 12 movements to light the blue squares. Here we will see how easy it is to tell the robot to move forward, turn to the left or right, or jump to climb up a box.
When we finish the first level, we will see that 12 commands are insufficient to light all the blue boxes. At this time, it becomes an introduction to the concept of function or procedure that will allow us to group a certain number of commands and use them as a single command.
In level 3, the concept of a loop is explained, where we will see how to repeat a sequence of commands infinitely.

The game is available for iPad, iPhone, Android, and Web Browsers. iOS and Android versions are paid and contain 40 phases. The web version can be played on any browser that has installed the plug-in Flash Player. The web version is free of charge and only contains 18 phases. Even so, these 18 phases are more than enough for the children to learn programming fundamentals and do it fun and entertainingly.

At the top right of the main screen, we can select the language to display the game.

If you don't know how to solve some phases, you can look at the screenshots we made. Even so, trying to solve the phases without any external help is always advisable.